TEMA 5 ESTADÍSTICOS UNIVARIABLES

TEMA 5 ESTADÍSTICOS UNIVARIABLES:

 MEDIDAS RESUMEN PARA VARIABLES CUANTITATIVAS

MEDIDAS DE TENDENCIA CENTRAL. MEDIDAS DE DISPERSIÓN . MEDIDAS DE POSICIÓN. FORMA DE DISTRIBUCIÓN: ASIMETRÍA Y CURTOSIS

MEDIDAS DE TENDENCIA CENTRAL:

Dan idea de los valores alrededor de los cuales el resto de los datos tienen tendencia a agruparse.

Son: MEDIA, MEDIANA Y MODA.

-MEDIA ARITMÉTICA O MEDIA (x):

Es la suma de todos los valores de la variable observada entre el total de observaciones.

Es la medida mas calculada y utilizada en estadística descriptiva.

Propiedades de la media: 

1) La suma de las desviaciones respecto de la media es igual a cero.

2) La media no se altera por una transformación lineal de escala (si a los conjuntos de datos se le suma o multiplica un número, ese mismo número multiplica o suma el valor de la media también).

3) Es muy sensible a las puntuaciones extremas.

Hay otros tipos de medias pero son menos utilizada, entre ellas encontramos:

-Media geométrica: que se describe como la raíz enésima del producto de los N valores observados.

-Media armónica: inverso de la media aritmética de los inversos de los valores de las variables.

-Media aritmética ponderada: media aritmética de la suma del producto de cada valor por el peso o relevancia asignada al mismo.

-MEDIANA

Es la puntuación que ocupa la posición central de la distribución.

Es fundamental que los datos se encuentre ordenados de forma creciente o decreciente.

Si la media y la mediana son iguales, la distribución de la variable es simétrica.

A diferencia de la media, la mediana es más robusta y menos sensible a los valores extremos.

Cuando tenemos valores dispersos o son valores muy extremos se utiliza mas la mediana.

IMPORTANTE:

Si el número es impar el valor de la observación sera justamente la observación que ocupa la posición (n+1)/2.

Ejemplo: Juan tiene las siguientes notas en los examen: 5,6,7,8,9. La mediana seria 7.

Si el número es par, se tienen en cuenta los dos valores centrales ( no hay un único valor central debido a que es un número par) y lo que se hace es el valor promedio de los dos valores seleccionados.

Ejemplo: Juan ha comparado el precio de 10 zapatillas que son los siguientes: 22,40,53,57,93,98,103,108,116,121. En este caso se seleccionaría el 93 y 98 que son los valores centrales y hallaríamos el promedio, es decir :(93+98)/2=95,5.

-MODA

Es el valor con mayor frecuencia (que más veces se repite).

Las distribuciones que contienen una sola moda se llaman UNIMODALES, si hay más de una se dice que la muestra es BIMODAL y si es mas de dos se denomina MULTIMODAL.

En una distribución unimodal simétrica, los valores de la media, mediana y moda coinciden.

Ejemplo de distribución de frecuencia unimodal (12,14,14,18,25)

Ejemplo de distribución de frecuencia bimodal (20,24,24,27,28,28,29)

MEDIDAS DE POSICIÓN:

Dividen un conjunto ordenado de datos en grupos con las misma cantidad de individuos.

Son: CUARTILES, DECILES Y PERCENTILES, TODOS SE DENOMINAN CUANTILES.

• CUANTILES: Se define el cuantil de orden "n" como un valor de la variable por debajo del cual se encuentra una frecuencia acumulada n. Al igual que la mediana solo tiene en cuenta la posición de los valores de la muestra.

-PERCENTILES

Dividen la muestra ordenada en 100 partes y se reprentan por P(n).

Mas tarde realizaremos una actividad para que quede algo mas claro.

-DECILES

Dividen la muestra ordenada 10 partes.

Cada parte incluye el 10 % de los valores de la distribución.

Se representa por la D(n).

El valor del D(5) corresponde al valor de la mediana y por tanto al de P50.

-CUARTILES

Dividen la muestra ordenada en 4 partes. Son los tres valores que dividen la distribución en cuatro partes iguales, cada parte incluye el 25% de los valores de dicha variable.

Se reprenta por Q1,Q2 Y Q3.

MEDIDAS DE DISPERSIÓN:

Dan información acerca de la heterogeneidad de nuestras observaciones.
Son: RANGO, DESVIACIÓN, MEDIA, VARIANZA, DESVIACIÓN TÍPICA, COEFICIENTE DE VARIACIÓN.

-RANGO O RECORRIDO (R)

Es la medida de dispersión más simple y consiste en tomar la puntuación mayor y restarle la puntuación menor.
Es el recorrido de una variable.
Se ve dramáticamente afectado por los valores extremos ya que solo se tienen en cuenta los valores menores y mayores.

Por ejemplo si disponemos de los siguientes valores:
22,45,56,60,89,90 --- el recorrido seria 90-22=68

-DESVIACIÓN MEDIA (DM)
Es la media aritmética de las distancias de cada observación con respecto a la media de la muestra.

-VARIANZA(S2)
Es la media de los cuadrados de las diferencias entre cada valor de la variable y la media aritmética de la distribución.
Siempre tiene valor positivo.
Se mide en unidades de la variable estudiada.
Cuanto menor sea la varianza mayor homogeneidad y menor dispersión

-DESVIACIÓN TÍPICA O ESTÁNDAR (S)

Expresa la dispersión de la distribuciñon mediante un valor que siempre es positivo y en las mismas unidades de medida de la variable, siendo la medida de dispersión más utilizada den estadística descriptiva.
Cuando los datos están muy alejados de la media, el numerador será grande y la varianza y la desviación típico también lo serán.

Propiedades de la desviación típica:
1)Siempre proporciona un valor positivo o cero, en el caso de que las puntuaciones sean iguales.
2)Si a todos los valores de las variable se les suma o multiplica un número la desviación típica queda multiplica o sumada por ese número.

Observaciones de la desviación típica:
1)Al igual que la media y la varianza, es un índice muy sensible a las puntuaciones extremas.
2)En los casos que no se pueda hallar la media tampoco se puede calcular la desviación típica.
3)Mientras más pequeña es la desviación típica mayor será la concentración de datos alrededor de la media (mayor homogeneidad).

-COEFICIENTE DE VARIACIÓN (CV)

Es una medida adimensional que permite comparar la dispersión o variabilidad de dos o más grupos.
En cambio, no debe usarse cuando la variable presenta valores negativos o donde el valor sea una cantidad fijada aleatoriamente.

DISTRIBUCIONES NORMALES

También llamada DISTRIBUCIÓN GAUSSIANA, es una de las mas utilizadas en los fenómenos reales.
La gráfica de su función tiene una forma acampanada y es simétrica respecto de los valores de posición central (media, mediana y moda).

MEDIDAS DE FORMA: ASIMETRÍA Y CURTOSIS

Dichas medidas de forma indican si la distribución es simétrica y el grado de apuntamiento, tomando siempre como referencia la curva normal.

-ASIMETRÍAS

Coeficiente de asimetría : Grado de asimetría de la distribución de sus daros en torno a su media.
Las distribuciones asimétricas también se llaman sesgadas y se caracterizan porque el pico de la misma se encuentra descentrado apareciendo una cola mas larga que la otra
Es adimensional y adopta valores entre -1 y +1.

Interpretación del coeficiente de asimetría:

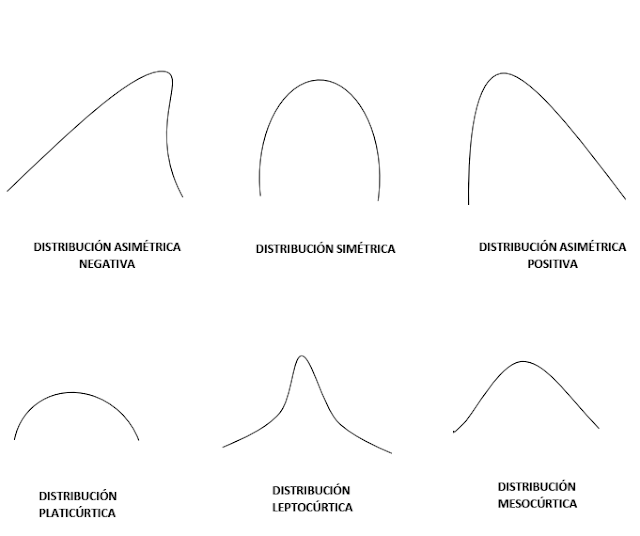
• g1=0---DISTRIBUCIÓN SIMÉTRICA: existe la misma concentración de valores a la derecha y a la izquierda de la media.
• g1>0---DISTRIBUCIÓN ASIMÉTRICA POSITIVA: la cola de la distribución es mas larga hacia la derecha y los valores más elevados quedan hacia la izquierda.
• g1<0---DISTRIBUCIÓN ASIMÉTRICA NEGATIVA: la cola de la distribución es mas larga hacia la izquierda y los valores más elevados quedan a la derecha.

-CURTOSIS O APUNTAMIENTO

Sirve para medir el grado de concentración de los valores que toma en torno a su media.
Se elige como referencia una variable de curtosis es 0.
Adopta también valores entre -1 y +1.

Los resultados pueden ser:

• g2=0--- DISTRIBUCIÓN MESOCÚRTICA: presenta un grado de concentración medio alrededor de los valores centrales de la variable.
• g2>0--- DISTRIBUCIÓN LEPTOCÚRTICA: presenta un elevado grado de concentración alrededor de los valores centrales de la variable.
• g2<0--- DISTRIBUCIÓN PLATICÚRTICA: presenta un reducido grado de concentración alrededor de los valores centrales de la variable.